Boyle-Mariotte law
The Boyle-Mariotte law or also called Boyle's law describes the relationship between pressure and volume of a predefined enclosed amount of gas at a constant temperature. It is the most important physical law for diving.
Contents
Basic knowledge for Open Water Diver* (OWD*)
Compressibility of gases and liquids
Gases are compressible unlike liquids. If you increase the pressure of an enclosed amount of gas, then its volume decreases. You can illustrate this with the following example:
Fill a disposable syringe half with water and half with air. Seal the inlet opening with a finger and then push the piston into it. On the one hand you will notice that the volume of the water does not change, whereas the volume of the air decreases. This means, the contained gas is compressable. On the other hand, the farther you push the plunger, the more force you will need to hold the tube outlet tight. This means you have increased the gas pressure by reducing the volume of the contained gas.
Relation between pressure and volume
A predefined amount of gas may have different volumes depending on the pressure it is exposed to. The product of pressure and volume corresponds to the amount of gas and this stays constant as long as the amount of gas is enclosed. Expressed in figures, a predefined amount of gas at double pressure has half the volume, at triple pressure one third of the volume, etc.
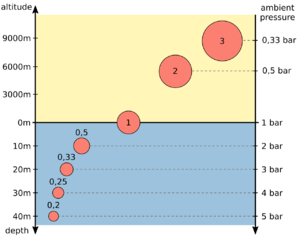
The balloon in the picture has a volume of 1 l at the water surface at an ambient pressure of 1 bar. If you dive with it to a depth of 30 m, it is compressed by the ambient pressure of 4 bar to a volume of 0.25 l. Since the balloon is flexible, the pressure inside the balloon equals the ambient pressure of 4 bar. If you would place it on a high mountain with an ambient pressure of only 0.5 bar, it would expanded to a volume of 2 liters. However, this does not change the amount of gas − the product of pressure and volume − inside the balloon.
Examples
For you as a diver, the relationship described by Boyle-Mariotte law, is very crucial in many ways:
- Your compressed air cylinder has a fixed volume and is filled with highly compressed air. For example a 10 liter cylinder filled with 200 bar contains 200 times the amount of the original tank volume. This amount of gas would have a volume of 2000 liters at ambient pressure.
- In order to be able to breathe under water, your breathing air must be at the same pressure as the prevailing ambient pressure in your diving depth. Because you inhale approximately the same volume with each breath, regardless of the depth of the dive, you need twice that amount at 10 m depth (2 bar ambient pressure) and three times that amount at 20 m depth (3 bar ambient pressure) compared to the water surface (1 bar ambient pressure). This means that the amount of air you consume depends on the depth of the dive.
- If you would take a deep breath, hold your it and then ascend, the air in your lungs would expand as the ambient pressure decreases. Your lungs would not withstand the pressure of the expanding air, like a overinflated balloon, you would suffer a pulmonary barotrauma. This results in one of the most important rules in diving: Never hold your breath!
- In your body are many more air-filled cavities, such as the paranasal sinuses or the middle ear, which are connected via small tubes with the nasopharyngeal space. The air in these cavities expands when ascending or is compressed on descent. If the channels are swollen or blocked by a cold, for example, pressure equalization is not possible and you will damage the mucous membranes in the cavities, eardrum or inner ear. Therefore, never dive with signs of a cold and tell your VIT instructor immediately, if you are in pain under water so he can safely end the dive with you.
- Also in buoyancy you will find Boyle's law: Your buoyancy under water is determined by the volume of air in your BCD. As you descend, the ambient pressure increases, the air in the BCD is compressed, its volume decreases, and you are less buoyant. You sink faster with decreasing volume of your BCD. Therefore, on descent you have to constantly add small amounts of air into your BCD to compensate for the loss on volume due to the compressing air. On ascend you have to compensate for expanding air and therefore increasing volume of your BCD and becoming increasingly positive buoyant by releasing air from your buoyancy control device.
Knowledge for Experienced Diver** (ED**)
Calculations
The Boyle-Mariotte law states that the product from pressure and volume of a predefined amount of gas remains constant.
If [math]p_1[/math] and [math]V_1[/math] are pressure and volume before a change in pressure and [math]p_2[/math] and [math]V_2[/math] are pressure and volume after it, the Boyle's law can be expressed with the following equation:
- [math]p_1 \cdot V_1 = p_2 \cdot V_2[/math]
To be balanced, you have to fill your BCD at 10 m depth, for example with a volume of 5 l of air. The amount of gas contained is:
- [math]p_1 \cdot V_1 = 2\ \text{bar} \cdot 5\ \text{l} = 10\ \text{barl}[/math]
If you dive to a depth of 15 m without changing the amount of gas in your buoyancy control device, the volume will decrease as the pressure increases. You can calculate the volume [math]V_2[/math] by transforming (divison by [math]p_2[/math]) the above equation:
- [math]V_2 = \frac{p_1 \cdot V_1}{p_2} = \frac{10\ \text{barl}}{2,5\ \text{bar}} = 4\ \text{l}[/math]
Depending on the density of the water, you are about 1 kg negative buoyant and continue to descend if you do not add air to your BCD.
If you would fill your lungs with a volume of 4 l of air, at 20 m depth, then your lungs would contain a gas volume of 12 barl:
- [math]p_1 \cdot V_1 = 3\ \text{bar} \cdot 4\ \text{l} = 12\ \text{barl}[/math]
If you would ascend all the way to the surface while holding your breath, then the air in your lungs would expand due to the reducing ambient pressure:
- [math]V_2 = \frac{p_1 \cdot V_1}{p_2} = \frac{12\ \text{barl}}{1\ \text{bar}} = 12\ \text{l}[/math]
This would exceed the extensibility of your alveoli and you would suffer a pulmonary barotrauma.
Knowledge for experts (DM***)
Ideal gas
Since here we used the model of the so called ideal gas. It is a hypothetical model whereby gas particles do not have any volume and do not influence each other. It is a good approximation of the behavior of many gases under various conditions. Boyle's law can be derived from the basic equation of this model:
- [math]\frac{p \cdot V}{T} = N \cdot k_B[/math]
With a predefined and enclosed amount of gas, the particle number [math]N[/math] remains the constant. If one keeps the temperature of the gas constant during a pressure or volume change, then the Boyle's law follows from it:
- [math]p \cdot V = \text{constant}[/math]
Real gas
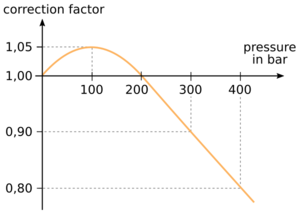
Real gas behavior deviates from ideal gas behavior under non-ideal conditions. They behave differently because these non-ideal conditions are pretty stressful - very high pressures and densities, and very low temperatures. In order to account for this change we need to modify the ideal gas law slightly. These changes include constants that quantify the volume of the gas molecules as well as the attractive forces between those molecules, both of which are considered negligible under ideal conditions.
In this case, the relationship pressure times volume is constant according to Boyle's law is not valid exactly anymore and a correction factor has to be taken into account in order to determine the gas volume from cylinders pressure and volume.
For example, a 10 l tank filled with 300 bar holds only a gas amount of 2700 barl. The correction factor at 300 bar is 0.9 as shown in the figure.
In the pressure range up to 200 bar actually a correction factor should be taken into account. However, the approximation without correction factor is sufficient for recreational diving, since the actual amount of gas can be slightly larger depending on the pressure than it was calculated with the approximation.